Introducción a las fibras ópticas, dB, atenuación y mediciones

Introducción

Este documento es una referencia rápida a algunas de las fórmulas y a información importante relacionada con las tecnologías ópticas. Este documento se centra en los decibelios (DB), los decibeles por milivatio (dBm), la atenuación y las mediciones, y proporciona una introducción a las fibras ópticas.

Prerequisites

Requirements

No hay requisitos específicos para este documento.

Componentes Utilizados

Este documento no tiene restricciones específicas en cuanto a versiones de software y de hardware.

La información que contiene este documento se creó a partir de los dispositivos en un ambiente de laboratorio específico. Todos los dispositivos que se utilizan en este documento se pusieron en funcionamiento con una configuración verificada (predeterminada). If your network is live, make sure that you understand the potential impact of any command.

Convenciones

Consulte Convenciones de Consejos TécnicosCisco para obtener más información sobre las convenciones del documento.

¿Qué es un decibel?

Un decibelio (dB) es una unidad utilizada para expresar las diferencias relativas en la potencia de la señal. Se expresa un decibelio como logaritmo decimal de la relación entre la potencia de dos señales, como se muestra aquí:

dB = 10 x Log10 (P1/P2)

donde Log10 es el logaritmo decimal y P1 y P2 son las potencias que se comparan.

Nota: Log₁₀ es diferente del logaritmo base e neperiano (Ln o LN).

También se puede expresar la amplitud de señal en dB. La potencia es proporcional al cuadrado de la amplitud de una señal. Por lo tanto, el dB se expresa como:

dB = 20 x Log10 (V1/V2)

donde V1 y V2 son las amplitudes que deben compararse.

1 Bell (no utilizado actualmente) = Log10 (P1/P2)

1 decibel (dB) = 1 Bell / 10 = 10 * Log10 (P1/P2)

dBr = dB (relativo) = dB = 10 * Log10 (P1/P2)

Reglas de los logaritmos decimales

• Log10 (AxB) = Log10 (A) + Log10 (B)

• Log10 (A/B) = Log10 (A) - Log10 (B)

• Log10 (1/A) = - Log10 (A)

• Log10 (0,01) = - Log10 (100) = -2

• Log10 (0,1) = - Log_{10(10) = - 1}

• Log10 (1) = 0

• Log10 (2) = 0,3

• Log10 (4) = 0,6

• Log10 (10) = 1

• Log10 (20) = 1,3

  Log10 (2 x 10) = Log10 (2) + Log10 (10) = 1 + 0,3

• Log10 (100) = 2

• Log10 (1000) = 3

• Log10 (10000) = 4

dB

Esta tabla enumera las relaciones de potencia logarítmicas y los valores en dB (decibelios):

Relación de potencia	dB = 10 x Log10 (relación de potencia)
AxB	x dB = 10 x Log10(A) + 10 x Log10(B)
A/B	x dB = 10 x Log10(A) - 10 x Log10(B)
1/A	x dB = + 10 x Log10 (1/A) = - 10 x Log10 (A)
0,01	- 20 dB = - 10 x Log10(100)
0,1	- 10 dB = 10 x Log10 (1)
1	0 dB = 10 x Log10 (1)
2	3 dB = 10 x Log10 (2)
4	6 dB = 10 x Log10 (4)
10	10 dB = 10 x Log10 (10)
20	13 dB = 10 x (Log10 (10) + Log10 (2))
100	20 dB = 10 x Log10 (100)
1000	30 dB = 10 x Log10 (1000)
10000	40 dB = 10 x Log10 (10000)

Decibelios referidos a un milivatio (dBm)

dBW = dB milivatios = 10 x Log10 (Energía en mW / 1 mW)

Energía	Proporción	dBm = 10 x Log10 (Potencia en mW / 1 mW)
1 mW	1 mW/1mW=1	0 dBm = 10 x Log10 (1)
2 mW	2 mW/1mW=2	3 dBm = 10 x Log10 (2)
4 mW	4 mW/1mW=4	6 dBm = 10 x Log10 (4)
10 mW	10 mW/1mW=10	10 dBm = 10 x Log10 (10)
0,1 W	100 mW/1mW=100	20 dBm = 10 x Log10 (100)
1 W	1000 mW/1mW=1000	30 dBm = 10 x Log10 (1000)
10 W	10000mW/1mW=10000	40 dBm = 10 x Log10 (10000)

Decibelios referidos a un vatio (dBW)

dBW = dB Vatios = 10 x Log10 (Energía en W / 1 W)

Energía	Proporción	dBm = 10 x Log10 (Potencia en mW / 1 mW)
1 W	1 W / 1 W = 1	0 dBW = 10 x Log10 (1)
2 W	2 W / 1 W = 2	3 dBW = 10 x Log10 (2)
4 W	4 W / 1 W = 4	6 dBW = 10 x Log10 (4)
10 W	10 W / 1 W = 10	10 dBW = 10 x Log10 (10)
100 mW	0,1 W / 1 W = 0,1	-10 dBW = -10 x Log10 (10)
10 mW	0,01 W / 1 W = 1/100	-20 dBW = -10 x Log10 (100)
1 mW	0,001W/1W=1/1000	-30 dBW = -10 x Log10 (1000)

Ganancias de suministro eléctrico/tensión

Esta tabla compara las potencias y las ganancias de voltaje:

dB	Relación de potencia	Proporción de voltaje	dB	Relación de potencia	Proporción de voltaje
0	1,00	1,00	10	10,00	3,16
1	1,26	1,12	11	12,59	3,55
2	1,58	1,26	12	15,85	3,98
3	2,00	1,41	13	19,95	4,47
4	2,51	1,58	14	25,12	5,01
5	3,16	1,78	15	31,62	5,62
6	3,98	2,00	16	39,81	6,31
7	5,01	2,24	17	50,12	7,08
8	6,31	2,51	18	63,10	7,94
9	7,94	2,82	19	79,43	8,91
10	10,00	3,16	20	100,00	10,00

Con esta información, puede definir las fórmulas para atenuación y ganancia:

Atenuación (dB) = 10 x Log_{10 (P entrada/P salida) = 20 x Log10 (V entrada/V salida)}

Ganancia (dB) = 10 x Log_{10 (P salida/P entrada) = 20 x Log10 (V salida/V entrada)}

Estructura de fibra óptica

La fibra óptica es un medio de transporte de información. La fibra óptica está hecha de vidrio a base de sílice y consta de un núcleo rodeado por un revestimiento. La parte central de la fibra, llamada núcleo, tiene un índice de refracción N1. El revestimiento que rodea al núcleo tiene un índice de refracción N2, más bajo. Cuando la luz ingresa en la fibra, el revestimiento confina la luz al núcleo y la luz recorre la fibra por reflexión interna entre los límites del núcleo y el revestimiento.

Figura 1: Estructura de la fibra óptica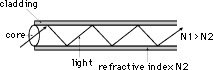

Tipo de Fibra

Las fibras monomodo (SM) y multimodo (MM) son las principales fibras que se fabrican y comercializan en la actualidad. La Figura 2 proporciona información sobre ambos tipos de fibra.

Figura 2: fibras MM y SM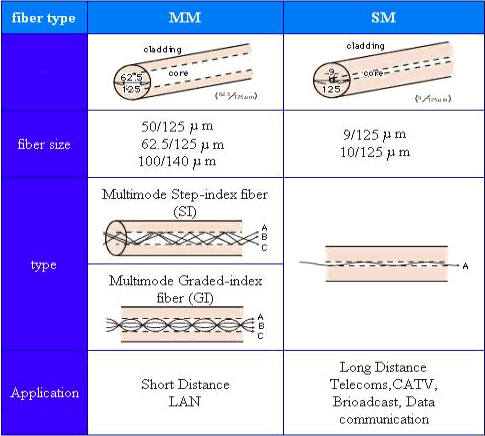

Wavelength

Una pequeña cantidad de luz se inyecta en la fibra. Esto genera una longitud de onda visible (de 400 nm a 700 nm) y una longitud de onda casi infrarroja (de 700 nm a 1700 nm) en el espectro electromagnético (vea la Figura 3).

Figura 3: Espectro electromagnético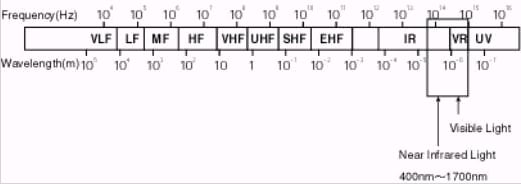

Hay cuatro longitudes de onda especiales que se pueden utilizar para la transmisión de la fibra óptica con niveles bajos de pérdida óptica. Se las enumera en esta tabla:

Windows:	Wavelength	Pérdida
primera longitud de onda	850nm	3dB/km
Segunda longitud de onda	1310nm	0.4dB/km
3er longitud de onda	1550nm (Banda C)	0.2dB/km
cuarta longitud de onda	1625nm (banda L)	0.2dB/km

Poder óptico

Para medir la pérdida óptica, puede utilizar dos unidades: dBm y dB. Mientras que dBm es el nivel de potencia real representado en milivatios, dB (decibelio) es la diferencia entre las potencias.

Figura 4: Cómo medir la potencia óptica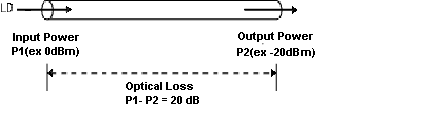

Si la potencia de entrada óptica es P1 (dBm) y la potencia de salida óptica es P2 (dBm), la pérdida de potencia es P1 - P2 dB. Para ver cuánta potencia se pierde entre la entrada y salida, consulte el valor dB en esta tabla de conversión de potencia:

dB	Salida de energía como % de entrada de energía	% de pérdida de potencia	Comentarios
1	79%	21%	-
2	63%	37%	-
3	50%	50%	1/2 de la potencia
4	40%	60%	-
5	32%	68%	-
6	25%	75%	1/4 de la potencia
7	20%	80%	1/5 de la potencia
8	16%	84%	1/6 de la potencia
9	12%	88%	1/8 de energía
10	10%	90%	1/10 de la potencia
11	8%	92%	1/12 de la potencia
12	6,3%	93,7%	1/16 de la potencia
13	5%	95%	1/20 de la potencia
14	4%	96%	1/25 de la potencia
15	3,2%	96,8%	1/30 de la potencia

Por ejemplo, cuando la entrada óptica de línea directa (LD) en la fibra es 0 dBm y la potencia de salida es -15 dBm, la pérdida óptica para la fibra se calcula como:

Input   Output    Optical Loss 
0dBm -  (-15dBm)  =15dB 

En la tabla de conversión de potencia, 15 dB para la pérdida óptica equivalen al 96,8% de la potencia óptica perdida. Por lo tanto, solamente queda un 3,2% de la potencia óptica cuando viaja por la fibra.

Comprender la pérdida por inserción

En cualquier interconexión de fibra óptica, ocurre una pérdida. La pérdida por inserción para un conector o empalme es la diferencia de potencia que se ve cuando se inserta el dispositivo en el sistema. Por ejemplo, tome una extensión de fibra y mida la potencia óptica a través de ella. Observe la lectura (P1). Ahora, corte la fibra por la mitad, instale la terminación adecuada a las fibras, conéctelas y mida la potencia otra vez. Observe la segunda lectura (P2). La diferencia entre la primera lectura (P1) y la segunda (P2) es la pérdida por inserción o la pérdida de potencia óptica que ocurre cuando inserta un conector en la línea. Esto se mide como:

IL (dB) = 10 Log10 (P2/P1)

Debe entender estos dos conceptos importantes sobre la pérdida por inserción:

• La pérdida de inserción especificada es para fibras idénticas.

  Si el diámetro del núcleo (o NA) del lado que transmite los datos es más grande que el NA de la fibra que recibe los datos, hay pérdida adicional.

  Ldia = 10 Log10 (diar/diat)²

  LNA = 10 Log10 (NAr/NAt)²

  where:

  • Ldia = diámetro de pérdida

  • diar = receptor del diámetro

  • diat = transmisión de diámetro

  • LNA = pérdida de fibra óptica

  Puede haber pérdida adicional por reflexión de Fresnel. Estas ocurren cuando dos fibras se separan de modo que existe una discontinuidad en el índice refractivo. Para dos fibras de vidrio separadas por una brecha de aire, la reflexión de Fresnel es de 0,32 dB.

• La pérdida depende de la inyección.

  La pérdida por inserción depende de las condiciones de inyección y recepción de las dos fibras que se unen. En una inyección corta, se puede desbordar la fibra con la energía óptica transportada tanto en el revestimiento como en el núcleo. Sobre la distancia, este exceso de energía se pierde hasta que la fibra alcanza una condición conocida como distribución de modo de equilibrio (EMD). En una inyección larga, la fibra ya ha alcanzado la distribución en modo de equilibrio (EMD), de manera que el exceso de potencia ya se eliminó y no está presente en el conector.

  La luz que cruza la unión fibra-fibra de una interconexión puede volver a desbordar la fibra con los modos excesivos del revestimiento, los que se pierden rápidamente. Esta es la condición de reducida recepción. Si se mide la salida de potencia de una fibra de recepción corta, se verá la energía adicional. Sin embargo, la energía adicional no se propaga lejos. La lectura es, por lo tanto, incorrecta. Asimismo, si la longitud de la fibra de recepción es lo suficientemente larga como para alcanzar la EMD, la lectura de la pérdida por inserción puede ser mayor, pero refleja las condiciones de la aplicación real.

  Puede simular fácilmente la EMD (inyección y recepción largas). Para esto, debe enrollar la fibra alrededor de un mandril cinco veces. Esto elimina los modos de revestimiento.

Calcular un presupuesto de potencia

Puede hacer un cálculo aproximado del presupuesto de potencia del enlace. Para esto, debe reservar 0,75 dB para cada conexión de fibra a fibra y suponer que la pérdida de la fibra es proporcional a la longitud de la fibra.

Para un tramo de 100 metros con tres paneles de conexión y una fibra de 62,5/125 con una pérdida de 3,5 dB/km, la pérdida total es de 2,6 dB, como se muestra aquí:

Fibra: 3,5 dB/km = 0,35 dB para 100 metros

Panel de conexión 1 = 0,75 dB

Panel de conexión 2 = 0,75 dB

Panel de parche 3 = 0.75 dB

Total = 2,6 dB

La pérdida medida es generalmente menor. Por ejemplo, la pérdida por inserción promedio para un conector SC AMP es de 0,3 dB. En este caso, la pérdida del enlace es solamente de 1,4 dB. Sin importar si ejecuta Ethernet a 10 Mbps o modo de transferencia asíncrona (ATM) a 155 Mbps, la pérdida es la misma.

La Reflectometría óptica en el dominio del tiempo (OTDR) es un método de certificación más utilizado para sistemas de fibra. El reflectómetro óptico en el dominio del tiempo (OTDR) inyecta luz en la fibra y muestra gráficamente los resultados de la luz reflejada. El OTDR mide el tiempo de tránsito transcurrido de la luz reflejada para calcular la distancia a diversos eventos. La representación visual permite determinar la pérdida por unidad de longitud, la evaluación de los empalmes y los conectores, y la ubicación de la falla. El OTDR se centra en ciertas ubicaciones para brindar una imagen en primer plano de las porciones del enlace.

Si bien puede utilizar medidores de potencia e inyectores de señal para muchas certificaciones y evaluaciones de enlaces, el OTDR proporciona una herramienta de diagnóstico potente para obtener una imagen completa del enlace. Pero el OTDR requiere una mayor capacitación y cierta habilidad para interpretar la imagen.

Información Relacionada

• Página de soporte de productos ópticos
• Soporte Técnico y Documentación - Cisco Systems