Definizione di voce analogica
Sommario
Introduzione
In questo documento viene descritto come vengono misurati i segnali vocali analogici, le unità utilizzate e i punti di riferimento utilizzati durante le misurazioni.
La qualità di un sistema di trasmissione è definita dalla differenza tra la voce parlata da un'estremità e la voce riprodotta dall'altra estremità. Chiunque utilizzi il telefono sperimenta sia buone che cattive connessioni, e può probabilmente descrivere la qualità di una particolare connessione in modo soggettivo. Ma come si può definire il bene e il male in modo obiettivo?
In trasmissione, il primo passo per rispondere a questa domanda è decidere su queste domande:
-
Cosa si deve misurare?
-
Quali sono le unità di misura?
-
Qual è il punto di riferimento per le misurazioni?
Questo documento risponde a queste domande.
Prerequisiti
Requisiti
Nessun requisito specifico previsto per questo documento.
Componenti usati
Il documento può essere consultato per tutte le versioni software o hardware.
Convenzioni
Fare riferimento a Cisco Technical Tips Conventions per ulteriori informazioni sulle convenzioni dei documenti.
Caratteristiche della voce analogica
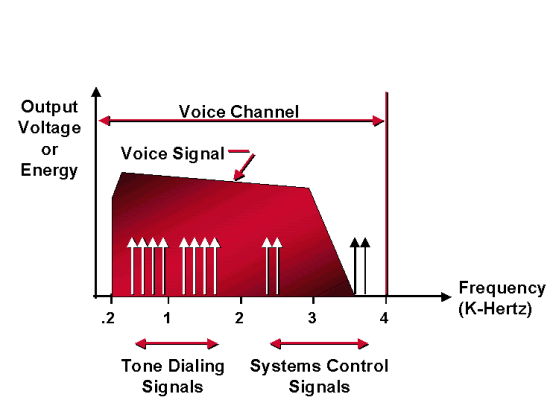
Analogico è definito come un segnale che ha un'ampiezza o una frequenza che varia in modo continuo e uniforme. Il linguaggio umano, e tutto ciò che si sente, è in forma analogica, e anche i primi sistemi telefonici erano analogici. I segnali analogici sono spesso rappresentati come onde sinusoidali uniformi, ma la voce e altri segnali sono più complessi di questo, poiché contengono molte frequenze. La figura della sezione Analog Voice Measurement mostra la tipica distribuzione di energia nei segnali vocali.
L'asse verticale è l'energia relativa, mentre l'asse orizzontale è la frequenza. La figura nella sezione Analog Voice Measurement (Misurazione voce analogica)mostra che le frequenze vocali che contribuiscono alla sintesi vocale possono estendersi da meno di 100 hertz a oltre 6000. Tuttavia, la maggior parte dell'energia necessaria per un discorso comprensibile è contenuta in una banda di frequenze tra 200 e 4000.
Al fine di eliminare i segnali indesiderati (rumore) che possono disturbare le conversazioni o causare errori nei segnali di controllo, i circuiti che trasportano i segnali telefonici sono progettati per passare solo determinate frequenze. Gli intervalli di frequenze passate si riferiscono alla banda passante. Da zero a 4000 hertz è la banda passante di un sistema telefonico di canale vocale-un canale VF. (A volte questa banda è chiamata canale di messaggio). La larghezza di banda è la differenza tra il limite superiore e il limite inferiore della banda passante. Pertanto, la larghezza di banda del canale VF è 4000 hertz. Tuttavia, la trasmissione della voce non richiede l'intero canale VF. La banda passante è limitata a 300-3300 hertz. Pertanto, qualsiasi segnale trasmesso sul circuito telefonico che sia compreso tra 300 e 3300 hertz viene chiamato segnale in banda. Qualsiasi segnale che non sia all'interno delle bande da 300 a 3300 hertz, ma all'interno del canale VF, è detto segnale fuori banda. Tutti i segnali vocali sono segnali in banda. Alcune trasmissioni di segnalazione sono in-band e altre fuori banda.
Misurazione voce analogica
Qualsiasi forma d'onda può essere caratterizzata in termini di frequenze e potenza. Le quantità comunemente utilizzate per descrivere vari aspetti delle prestazioni della trasmissione sono la frequenza e la potenza. Molti standard di prestazioni sono espressi in termini di potenza a una particolare frequenza. L'unità usata per misurare la frequenza è l'hertz, abbreviato in Hz o visto con il simbolo f. Hertz è uguale a un ciclo (0,0000000125) o a un'oscillazione al secondo e misura le onde o le frequenze dei cambiamenti elettrici ogni secondo.
Come è comune nella maggior parte dei sistemi elettrici, la potenza è misurata in unità di watt, abbreviato W. Poiché la potenza riscontrata nei sistemi di trasmissione è relativamente piccola (rispetto alla potenza di una lampadina), la potenza è generalmente espressa in milliwatt, abbreviato mW.
1 mW = 1 W = 0.001W = 10–3W
————
1000
Nella trasmissione, l'interesse comune è rappresentato dai rapporti di potenza piuttosto che dalla potenza assoluta. Inoltre, la trasmissione riguarda una gamma estremamente ampia di valori di potenza assoluti. Per questi motivi, una comoda espressione matematica di potenza relativa, il decibel (dB), è comunemente usato. Per descrivere la potenza relativa in termini di decibel, dovete definire il punto di riferimento da cui misurate. In base al parametro di trasmissione misurato, è possibile utilizzare diverse forme di misurazione dei decibel. Ogni forma di misurazione ha un punto di riferimento definito in modo specifico. Quando si utilizzano le unità di potenza appropriate relative a riferimenti specifici, è possibile misurare la potenza assoluta, la potenza relativa e gli incrementi e le perdite di potenza.
Milliwatt e Hertz
Poiché la potenza nei circuiti telefonici è ridotta, il milliwatt viene utilizzato come unità di misura della potenza di base, così come il piede viene utilizzato come misura di base della lunghezza. La maggior parte delle misurazioni della potenza assoluta nella trasmissione sono effettuate in milliwatt o in unità direttamente correlate ai milliwatt.
Le frequenze utilizzate per il test rientrano in genere nella banda di frequenza della voce. I toni di prova puri (sinusoidali) comunemente usati sono 404 Hz, 1004 Hz e 2804 Hz. (L'offset a 4 Hz non è sempre indicato. Tuttavia, le frequenze di prova effettive dovrebbero essere scostate di 4 Hz per compensare gli effetti che alcune strutture portanti hanno sui toni di prova.) Una misura di 1004 Hz è vicina alle frequenze della banda vocale che trasportano molta potenza della voce, 404 Hz è vicino alla fascia bassa dello spettro e 2804 Hz è nella gamma di componenti a frequenza più alta dello spettro vocale che sono importanti per l'intelligibilità del linguaggio.
Oltre ai toni di prova puri, per alcune prove viene utilizzato il "rumore bianco" all'interno di specifiche gamme di frequenza. I toni di prova del rumore bianco sono forme d'onda complesse che hanno la loro potenza uniformemente distribuita sulla gamma di frequenza di interesse. "Rumore bianco" è un segnale che contiene tutte le frequenze audio in quantità uguali, ma che non manifesta toni o toni riconoscibili
Questa figura mostra, in modo molto generale e semplificato, come è impostata una trasmissione tono di prova e come sono generati e misurati i toni di prova (da demarc A a demarc B).
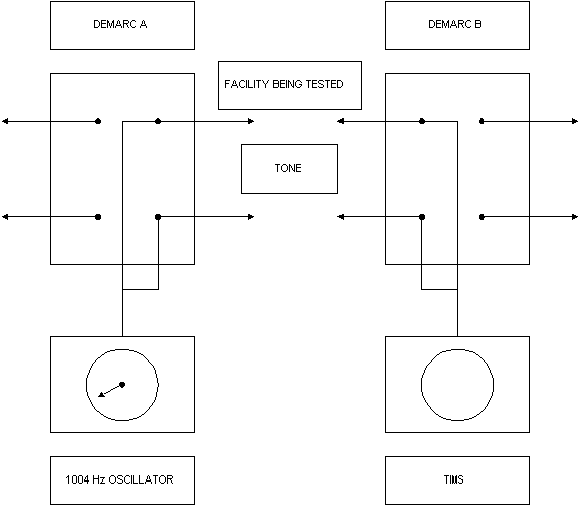
L'apparecchiatura è configurata per testare il circuito tra il demarc a A e il demarc a B. Si sta per misurare la perdita di 1004 Hz inerente al circuito tra A e B.
Le clip di bridging in entrambe le fasi vengono rimosse per isolare il segmento del circuito in prova.
In A, un oscillatore è collegato per trasportare e ricevere le spie (chiamate anche spie di punta e di anello). Alla lettera B, è collegato un ricevitore di misurazione della trasmissione (TIMS) per trasmettere e ricevere i cavi.
L'oscillatore a A è impostato per generare un tono di prova puro con una potenza di 1 mW a 1004 Hz. Alla demarc B, il TIMS è impostato sulla potenza di lettura nell'intervallo di 1 mW. La potenza di lettura a B è di 0,5 mW. Pertanto, la potenza persa tra A e B è:
1 mW – 0.5 mW = 0.5 mW
Un modo più utile per esprimere la perdita è in termini di perdita relativa, o il rapporto tra l'uscita di corrente (B) e l'entrata di corrente (A):
Relative loss = Power out (B)
——————————————
Power in (A)
Relative loss = 0.5 x 10-3
——————————————
1 X 10-3
Relative loss = 0.5
Half the power that the 1004 Hz test-tone introduced at A is lost by the time
it reaches B.
Nell'esempio seguente il test viene ripetuto con l'utilizzo di una minore potenza del tono di prova. L'oscillatore a demarc A è impostato per generare un tono di 1004 Hz ad una potenza di 0,1 mW. Alla demarc B, la misurazione della potenza è di 0,05 mW. La perdita di potenza assoluta è:
0.1 mW – 0.05 mW = 0.05 mW
La perdita relativa o il rapporto tra l'uscita di corrente (B) e l'ingresso di corrente (A) è:
Relative Loss = Power out(B)
——————————————
Power in (A)
Relative Loss = 0.05 x 10-3
—————————————
1 x 10-3
Relative Loss = 0.5
La perdita relativa, o rapporto di potenza tra B e A, è la stessa se si usa un segnale di prova di 1 mW o 0,1 mw.
Decibel
Matematicamente, il decibel è una misura logaritmica. Il logaritmo, o log, di un determinato numero è la potenza matematica alla quale un numero di base deve essere elevato per ottenere il numero specifico. Il numero di base utilizzato per il decibel è 10. Ad esempio, qual è il logaritmo (log) di 100? Un altro modo per porre questa domanda è 'A quale potere ne eleva 10 per ottenere 100?'. La risposta è 2 perché 10 x 10 = 100.
Analogamente,
log (100)= 2
log (1000)= 3
log (10,000)= 4
e così via.
È inoltre possibile utilizzare i logaritmi per esprimere quantità frazionarie. Ad esempio, qual è il logaritmo di 0,001? Un altro modo per porre questa domanda è 'A che potere si eleva 1/10 (0,1) per ottenere 0,001?'. La risposta è 3. Per convenzione, il log di un numero frazionario è espresso come negativo.
log (0.001) = -3
I logaritmi di numeri che non sono potenze integrali di 10 possono essere calcolati quando li si cerca in una tabella o quando si utilizza una calcolatrice manuale.
I decibel utilizzano i logaritmi per esprimere i rapporti di potenza. Per definizione, il deciBel, o dB, è il rapporto logaritmico (base 10) di due potenze, P1 e P2 dato da:
dB = 10 log P2
——
P1
P2 e P1 sono misurazioni della potenza espresse in unità coerenti. Il numero di decibel è positivo se P2 è maggiore di P1. Il numero è negativo se P1 è maggiore di P2 (vedere la tabella). È importante che le due potenze siano espresse nelle stesse unità, come milliWatt (mW) o Watt (W). In caso contrario, si verificheranno errori di calcolo.
| Rapporto di alimentazione | Valore dB |
|---|---|
| 2 | 3* |
| 4 | 6* |
| 8 | 9* |
| 10 | 10 |
| 100 | 20 |
| 1000 | 30 |
| 100000 | 50 |
| 1000000000 | 90 |
* Valore dB approssimativo.
Il rapporto di potenza tra la potenza misurata a B e la potenza misurata a A è di mezzo. Espresso in decibel:
(Loss, A to B) = 10 log (0.5) (Loss, A to B) = –3 dB
Con l'uso dei decibel, è possibile esprimere la perdita o il guadagno di un circuito o di un'apparecchiatura senza dover dichiarare esplicitamente i valori effettivi della potenza in ingresso e in uscita. Nell'esempio, la perdita tra A e B è sempre 3 dB, indipendentemente dalla quantità assoluta di potenza trasmessa.
Misura decibel relativa a un milliwatt
La potenza assoluta è espressa in milliwatt e la potenza relativa in decibel. Quando si stabilisce una relazione tra il decibel e il milliwatt, è possibile eliminare il milliwatt come unità di misura operativa e considerare esclusivamente il decibel e le unità di misura correlate. L'unità di misura utilizzata per esprimere la potenza assoluta in termini di decibel è dBm.
dBm = 10 log (Power, measured in mW)
—————————————————————————
1 mW
Poiché un milliwatt è il riferimento di potenza standard nelle comunicazioni, è logico che 0 dBm (il riferimento di potenza assoluto quando vengono utilizzate le unità decibel) sia uguale a 1 mW di potenza. Matematicamente:
0 dBm = 10 log Power out
——————————
Power in
0 dBm = 10 log (1/1)
0 dBm = 10 x 0 = 0
Poiché la potenza è una forma d'onda di corrente alternata e l'impedenza può variare in funzione della frequenza, è necessario indicare su quale frequenza si basa lo standard 0 dBm. La frequenza standard è 1004 Hz.
È inoltre necessario conoscere la resistenza o l'impedenza (carico) del circuito. L'impedenza standard è 600 Ohm.
Pertanto, il riferimento di 0 dBm è uguale a 1 mW di potenza imposta su un'impedenza di 600 Ohm di una frequenza di 1004 Hz.
Le prove sono in genere effettuate utilizzando segnali di prova meno potenti di 1 mW (0 dBm). Se si applica un tono di prova di 1004 Hz pari a -13 dBm ad A, si legge -16 dBm sul TIMS ad B. La perdita è ancora di -3 dB.
Punto del livello di trasmissione
In ogni discussione sulle prestazioni di un circuito, è necessario descrivere la potenza in un particolare punto di un circuito con riferimento alla potenza presente in altri punti del circuito. Tale potenza può essere la potenza del segnale, il rumore o i toni di prova.
La descrizione di questa potenza è simile a quella dell'altezza di una montagna (o della profondità dell'oceano). Per misurare l'altezza di una montagna, è necessario scegliere un'altezza di riferimento da cui misurare. L'altezza di riferimento standard è il livello del mare, a cui viene assegnata arbitrariamente un'altezza pari a zero. Quando si misurano tutte le montagne dal livello del mare, si possono fare confronti tra le loro altezze anche se possono essere distanti molti chilometri.
La figura mostra la trasmissione del tono di prova da demarc A a demarc B.

Analogamente, la potenza in punti specifici di un circuito può essere descritta in termini di potenza in un punto di riferimento standard.
Questo punto, che è analogo al livello del mare, è chiamato punto di livello di trasmissione zero, o TLP 0.
Qualsiasi altro TLP può essere riferito al TLP 0 sommando algebricamente i guadagni e le perdite a 1004 Hz dal TLP 0 al punto di misurazione.
La potenza presente in un particolare punto di un circuito dipende dalla potenza alla fonte del segnale, da dove viene applicata la fonte e dalla perdita o dal guadagno tra i due punti in questione.
Con l'uso del concetto di TLP 0, la potenza in un circuito viene descritta indicando quale sarebbe la potenza se fosse misurata con precisione al TLP 0. La notazione standard è dBm0, che indica la potenza a cui si riferisce la TLP 0.
Ad esempio, il termine -13 dBm0 indica che la potenza a 0 TLP è -13 dBm. Un TIM impostato correttamente misura -13 dBm al TLP 0. Esempio di segnale -13 dBm0.
Una volta individuata la potenza a 0 TLP, è possibile determinare facilmente la potenza in qualsiasi altro punto del circuito. Ad esempio, se il segnale è -13 dBm se misurato a 0 TLP, è l3 dB al di sotto del valore numerico di qualsiasi TLP sul circuito se misurato a tale TLP.
Se il segnale è -13 dBm a 0 TLP (lo rende un segnale -13 dBm0), allora la potenza a +5 TLP può essere calcolata come segue:
(TLP) + (Power at the 0 TLP) = Power at the +5 TLP) (+5)+(–13 dBm0) = –8 dBm
Se il segnale -13-dBm0 viene misurato correttamente a +5 TLP, il misuratore legge -8 dBm.
Analogamente, se si misura un segnale -13-dBm0 a -3 TLP, il misuratore legge -16 dBm:
(TLP) + (Power at the 0 TLP) = (Power at the –3 TLP) (–3)+(–13 dBm0) = –16 dBm
Per determinare la potenza prevista a ogni dato TLP, è sufficiente conoscere la potenza presente a qualche altro TLP nel circuito. E proprio come la montagna non deve essere vicina al mare per determinare la sua altezza, lo 0 TLP non deve esistere sul circuito.
La figura mostra un circuito tra due demarcatori. Al -16 TLP viene applicato un segnale tono di prova di -29 dBm. Quali sono i valori da misurare con +7 TLP?
Anche se il TLP 0 non esiste sul circuito, è possibile descrivere la potenza che si vede al TLP 0 se esiste:
TLP)+(Power at 0 TLP) = (Power at the –16 TLP)
(–16)+(Power at 0 TLP) = –29 dBm
(Power at 0 TLP) = –13 dBm
Utilizzando nuovamente la relazione, è possibile determinare la potenza al + 7 TLP:
(TLP)+ (Power at 0 TLP) = (Power at + 7 TLP) (+7)+(–13 dBm0) = –6 dBm
L'uso del riferimento 0 TLP consente di indicare gli obiettivi di trasmissione e i risultati misurati indipendentemente da qualsiasi TLP specifico e senza specificare quali saranno i livelli di tono di prova o dove applicare il tono di prova.
La figura mostra una trasmissione del tono di prova da demarc A a demarc B.

Unità di misura del rumore
Oltre alla descrizione della potenza del tono di prova in vari punti di un circuito, le unità di misura relative ai decibel possono essere utilizzate per descrivere il rumore presente in un circuito.
dBrn
Per descrivere la potenza in un circuito, si usa il termine dBm, che significa "potenza riferita a 1 mW". Poiché il rumore in genere contiene meno di 1 mW di potenza, è opportuno utilizzare una potenza di riferimento molto inferiore a 1 mW. La potenza di riferimento utilizzata nella descrizione del rumore è -90 dBm. La notazione utilizzata per descrivere il rumore in termini di rumore di riferimento è dBrn. Se si conosce il livello di rumore in dBm, è possibile misurare facilmente il rumore in dBm:
dBrn = dBm + 90 dB
Ad esempio, una misurazione del rumore di 30 dBn indica un livello di potenza di -60 dBm (30 dB al di sopra del livello di rumore di riferimento di -90 dBm). Nella tabella seguente viene illustrata la relazione tra dBm0 e dBrn.
| dBm0 | Valore dB |
|---|---|
| 0 | 90 |
| -10 | 80 |
| -20 | 70 |
| -30 | 60 |
| -40 | 50 |
| -50 | 40 |
| -60 | 30 |
| -70 | 20 |
| -80 | 10 |
| -90 | 0 |
DBrnC
Il rumore contiene numerose forme d'onda irregolari che hanno un'ampia gamma di frequenze e potenze. Anche se qualsiasi rumore sovrapposto a una conversazione ha un effetto interferente, gli esperimenti hanno dimostrato che l'effetto interferente è maggiore nella banda di frequenza media della voce.
Per ottenere una misura utile dell'effetto interferente del rumore, le varie frequenze che contribuiscono al rumore complessivo sono ponderate in base al loro effetto interferente relativo. Questa ponderazione viene effettuata mediante l'uso di reti di ponderazione, o filtri, all'interno di TIMS.
Le misurazioni del rumore attraverso una rete di ponderazione del messaggio C sono espresse in unità dBrnC (rumore al di sopra del rumore di riferimento, ponderazione del messaggio C).
DBrnCO
Come per la potenza del tono di prova, la potenza del rumore può essere riferita al TLP 0.
Ad esempio, se l'obiettivo del rumore per il circuito è 31 dBrnC0, qual è la misurazione del rumore con +7 TLP?
TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(+7) + (31 dBrnC0) = 38 dBrnC
La misurazione del rumore a +7 TLP è 38 dBrnC.
Qual è la misurazione del rumore con -16 TLP?
(TLP) + (Noise at the 0 TLP) = (Noise at TLP)
(–16) + (31 dBrnC0) = 15 dBrnC
La misurazione del rumore a -16 TLP è 15 dBrnC.
 Feedback
Feedback